

ONE TAIL HYPOTHESIS TEST CALCULATOR CODE
Modifying this code slightly: def welch_ttest(x1, x2,alternative):
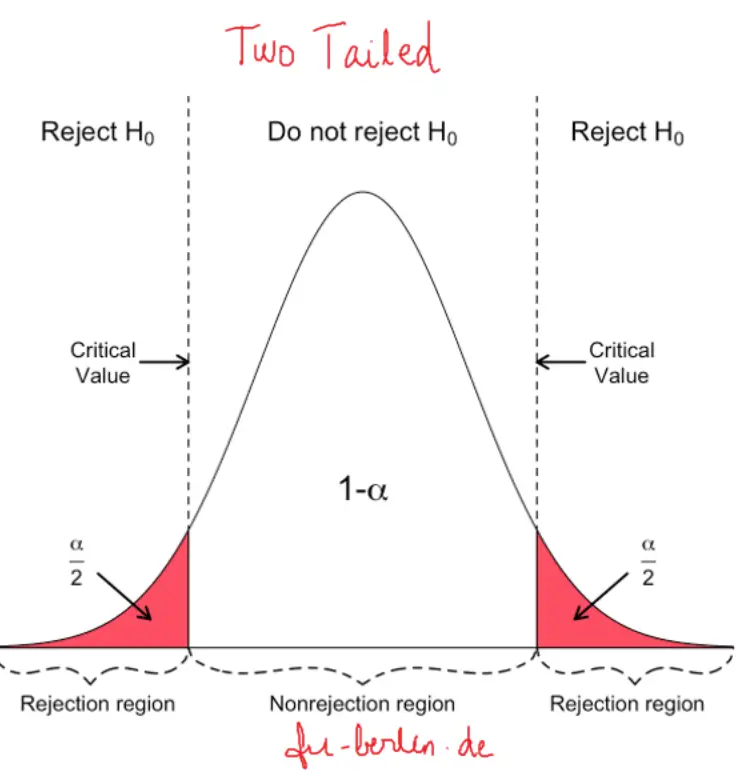
To do a one sided t test, you can use the cdf, which is the sum of probabilities up to your t statistic. ttest_ind performs a two sided test, which gives the probability that you observe something more extreme than the absolute of your t-statistic. You are correct, if you are doing a one sided test, it should have a large p-value. I would appreciate any additional help and guidance. Therefore, I feel like I'm either interpreting the results incorrectly or need to additional calculations to get the correct answer. However, my intuition tells me that the null hypothesis should not be rejected, because mu_2 is clearly larger than mu_1 (at the very minimum I would expect the p-value to be larger). The alpha value is 0.05, and the p-value is much much smaller than that which would mean the null hypothesis is rejected.
ONE TAIL HYPOTHESIS TEST CALCULATOR HOW TO
Given that scipy only takes into account a two-tail test, I am not sure how to interpret the values. I am using scipy to perform a two-sample t-test: stats.ttest_ind(data1, This is true, for example, for the t test. Equivalently, you can use the one-tailed p-value of. 04, which you can compare with alpha (say. Step 6 - Click on Calculate button to calculate f test for two. Step 4 - Enter the level of Significance ( ) Step 5 - Select the left tailed or right tailed or two tailed for f test calculator. 02, then for a symmetric distribution the p-value for the two-tailed test is. Step 3 - Enter the Standard Deviation for sample1 and sample2. I am working with a large dataset, but if I were to extract and round the parameters, for data_1 it is mu_1 = 4.3, s_1 = 4.8, and n_1 = 40000 and data_2 it is mu_2 = 4.9, s_2 = 4.4, n_2 = 30000. If the p-value for the one-tail test is say. Or should the null hypothesis still be that mu_1 - mu_2 = 0, even for the one-tailed case? I would like the null hypothesis to be that mu_2 > mu_1 and the alternative hypothesis to be mu_1 <= mu_2. It will compute the t-statistic, p-value, and evaluate if we should accept or reject the proposed hypothesis. For the specific problem I am looking, I want the comparison to only be in one direction. Adjust the calculator's settings (expected population mean, significance level, one or two tailed test) to match the test goals. I want to perform a two-sample, one-tailed t-test to compare two means. one-tailed (directional) and two-tailed (non-directional) hypotheses, and the one-tailed and two-tailed probability values associated with the test.


 0 kommentar(er)
0 kommentar(er)
